Splitting a Vector into two

A vector has an effect in any direction except the one at right angles to it. Sometimes a vector has two independent effects which need to be isolated. Just as the combined effect of two vectors acting on a single object can be calculated, two separate effects of a single vector can be found by splitting the vector into two components. Provided that the directions of the two components are chosen to be at right angles, each one has no effect in the direction of the other so they are

considered to act independently.

The process of splitting a vector into two components is known as resolving or resolution of the vector.

The diagram shows the tension (T) in a cable holding a radio mast in place. The force is pulling the mast both vertically downwards and horizontally to the left.

Image

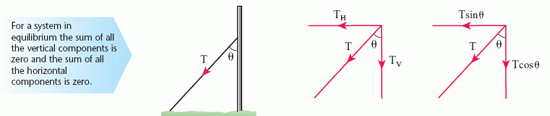
To find the effect of the tension in these directions, T can be split into two components, shown as T_H (the horizontal component) and T_V (the vertical component) in the diagram. You should check that according to the rules of vector addition, T_H + T_V = T.

To find the magnitude of T_H and T_V the following rules apply:

the component of a vector a at an angle θ to its own angle is acosθ

the component of a vector a at an angle (90° – θ) to its own angle is asinθ

The application of these rules is shown in the right-hand diagram above.