Angles

Angles are measured in degrees, written °. The maximum angle is 360°. This is the angle all the way round a point. Half of this is the angle on a straight line, which is 180°.

The video below explains how to calculate related angles, adjacent angles, interior angles and supplementary angles.

Related Angles

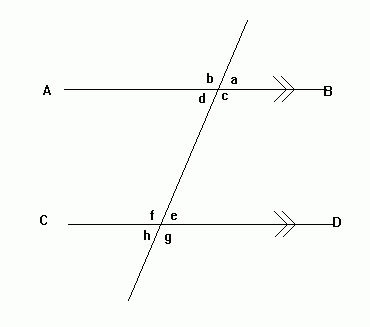
Lines AB and CD are parallel to one another (hence the » on the lines).

a and d are known as vertically opposite angles. Vertically opposite angles are equal. (b and c, e and h, f and g are also vertically opposite).

g and c are corresponding angles. Corresponding angles are equal. (h and d, f and b, e and a are also corresponding).

d and e are alternate angles. Alternate angles are equal. (c and f are also alternate). Alternate angles form a 'Z' shape and are sometimes called 'Z angles'.

a and b are adjacent angles. Adjacent angles add up to 180 degrees. (d and c, c and a, d and b, f and e, e and g, h and g, h and f are also adjacent).

d and f are interior angles. These add up to 180 degrees (e and c are also interior).

Any two angles that add up to 180 degrees are known as supplementary angles.

Angle Sum of a Triangle

Using some of the above results, we can prove that the sum of the three angles inside any triangle always add up to 180 degrees.

If we have a triangle, you can always draw two parallel lines like this:

Now, we know that alternate angles are equal. Therefore the two angles labelled x are equal. Also, the two angles labelled y are equal.

We know that x, y and z together add up to 180 degrees, because these together is just the angle around the straight line. So the three angles in the triangle must add up to 180 degrees.

Angle Sum of a Quadrilateral

A quadrilateral is a shape with 4 sides.

Now that we know the sum of the angles in a triangle, we can work out the sum of the angles in a quadrilateral.

For any quadrilateral, we can draw a diagonal line to divide it into two triangles. Each triangle has an angle sum of 180 degrees. Therefore the total angle sum of the quadrilateral is 360 degrees.

Exterior Angles

The exterior angles of a shape are the angles you get if you extend the sides. The exterior angles of a hexagon are shown:

A polygon is a shape with straight sides. All of the exterior angles of a polygon add up to 360°. because if you put them all together they form the angle all the way round a point:

Therefore if you have a regular polygon (in other words, where all the sides are the same length and all the angles are the same), each of the exterior angles will have size 360 ÷ the number of sides. So, for example, each of the exterior angles of a hexagon are 360/6 = 60°.

Interior Angles

The interior angles of a shape are the angles inside it. If you know the size of an exterior angle, you can work out the size of the interior angle next to it, because they will add up to 180° (since together they are the angle on a straight line).

Exterior Angle of a Triangle

Angle x is an exterior angle of the triangle:

The exterior angle of a triangle is equal to the sum of the interior angles at the other two vertices. In other words, x = a + b in the diagram.

Proof:

The angles in the triangle add up to 180 degrees. So a + b + y = 180.
The angles on a straight line add up to 180 degrees. So x + y = 180.
Therefore y = 180 - x. Putting this into the first equation gives us: a + b + 180 - x = 180. Therefore a + b = x after rearranging. This is what we wanted to prove.

Log in