Binary trees

After studying this section you should be able to:

explain the concept of a binary tree
describe methods of representing a binary tree
describe the algorithms used to manipulate a binary tree

Structure and use of binary trees

The data structure illustrated in below is a binary tree. In a binary tree, a node can have no more than two descendants.

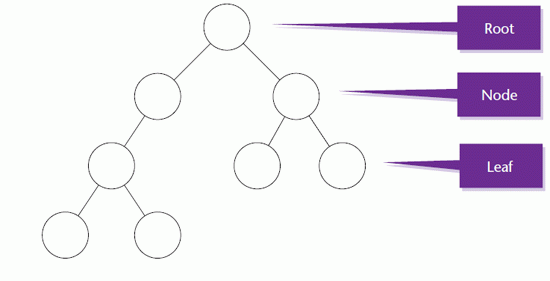
There are many types of tree but you should only meet binary trees on this course.

The descendants are known as the left child, or left descendant, and right child, or right descendant

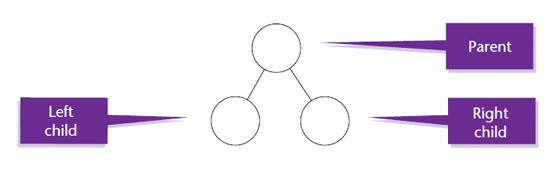
A binary tree node is like a linked list node but with two pointers, LeftChild and RightChild.

Binary trees can be used in many ways. One use is to hold an ordered set of data. In an ordered binary tree all items to the left of the root will have a smaller key than those on the right of the root. This applies equally to all the sub-trees. An example is:

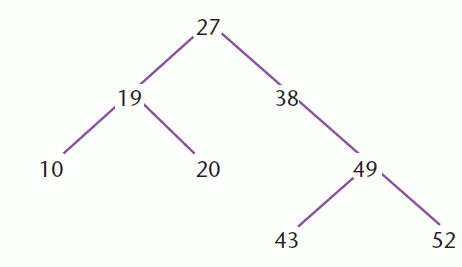
Tree algorithms are invariably recursive.

To insert data into an ordered tree the following recursive algorithm can be used:

PROCEDURE insert(Tree, Item)

     IF Tree is empty THEN create new tree with Item as the root.

     ELSE      IF Item < Root

          THEN insert(Left sub-tree of Tree, Item)

          ELSE insert(Right sub-tree of Tree, Item)

       ENDIF

     ENDIF

ENDPROC

Another common use of a binary tree is to hold an algebraic expression, for example:

X + Y * 2

could be stored as:

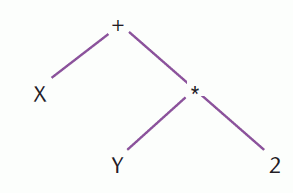
Binary trees can be traversed in three different orders: pre-order, in-order and postorder.

Pre-order traversal

The name pre-order comes from the use of binary trees to store expressions. The pre-order traversal produces the operators before the items. Pre-order is defined as:

visit the root node
traverse the left sub-tree
traverse the right sub-tree.

A procedure to output the tree T in pre-order can be written in pseudocode as:

PROCEDURE PREORDER(T)

     PRINT(Contents of the root node)

     PREORDER(Left sub-tree of T)

     PREORDER(Right sub-tree of T)

ENDPROC

The result if applied to the tree above is + X * Y 2.

In-order traversal

An in-order traversal produces the operators between the items and is defined as:

traverse the left sub-tree
visit the root node
traverse the right sub-tree.

An in-order traversal will produce an expression in the form that you are used to. The operators come between the items.

Post-order traversal

A post-order traversal places the operators after the items and is defined as:

traverse the left sub-tree
traverse the right sub-tree
visit the root node.

You may also know postorder as reverse polish.

Log in