Vectors

See also: vectors in the GCSE section and vectors in the Mechanics section.

A vector quantity has both magnitude and direction. Acceleration, velocity, force and displacement are all examples of vector quantities. A scalar quantity is has only magnitude (so the direction is not important). Examples include speed, time and distance.

Unit Vectors

A unit vector is a vector which has a magnitude of 1. There are three important unit vectors which are commonly used and these are the vectors in the direction of the x, y and z-axes. The unit vector in the direction of the x-axis is i, the unit vector in the direction of the y-axis is j and the unit vector in the direction of the z-axis is k.

Writing vectors in this form can make working with vectors easier.

The Magnitude of a Vector

The magnitude of a vector can be found using Pythagoras's theorem.

• The magnitude of ai + bj = √(a² + b²)

We denote the magnitude of the vector a by | a |

Position Vectors

Position vectors are vectors giving the position of a point, relative to a fixed point (the origin).

For example, the points A, B and C are the vertices of a triangle, with position vectors a, b and c respectively:

Image

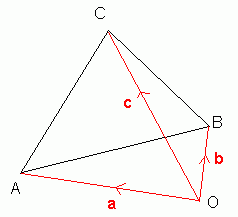
You can draw in the origin wherever you want. 

Notice that

Image

= - a + b = b - a because you can get from A to B by going from A to O and then going from O to B.

Vector Equation of a Line

The vector equation of a line passing through the point a and in the direction d is:

• r = a + td , where t varies.

This means that for any value of t, the point r is a point on the line.

If we are given the vector equations of two different lines, we can work out where the lines cross from their equations.

Example

Find where the lines with equations r = i + j + t (3i - j) and r = -i + s (j) intersect.

When they intersect, we can set the equations equal to one another:

i + j + t (3i - j) = -i + s (j)

Equating coefficients:

1 + 3t = -1 and 1 - t = s

So t = -2/3 and s = 5/3

The position vector of the intersection point is therefore given by putting t = -2/3 or s = 5/3 into one of the above equations. This gives -i +5j/3 .

Scalar Product

Suppose we have two vectors:

ai + bj + ck and di + ej + fk, then their scalar (or dot) product is: ad + be + fc. So multiply the coefficients of i together, the coefficients of j together and the coefficients of k together and add them all up.

Note that this is a scalar number (it is not a vector).

We write the scalar product of two vectors a and b as a·b.

Example

If a = i + 4j - 2k and b = 2i + 4j + 6k, then a·b = 2 + 16 - 12 = 6

Angle Between Two Vectors

We can use the scalar product to find the angle between two vectors, thanks to the following formula:

• a·b = |a| | b | cosq, where q is the angle between a and b

An important fact is that two vectors are perpendicular (orthogonal) if and only if their dot product is zero. This is because if q = 90 degrees above, then a·b = 0.