Game theory

After studying this section you should be able to:

understand the idea of a zero-sum game and its representation using a pay-off matrix
identify play-safe strategies and stable solutions
find optimal mixed strategies for a game with no stable solution
reduce a pay-off matrix using a dominance argument

A two person zero-sum game

The starting point in the mathematical theory of games is that the outcome of a game is determined by the strategies of the players.

A two person zero-sum game is a game in which the winnings of one player equal the losses of the other for every combination of strategies. Taking winnings to be positive and losses to be negative gives a zero sum in each case. Viewing a game from one player’s point of view, we could represent the outcomes (called pay-offs) for each combination of strategies in a matrix. This is called the pay-off matrix for that player.

Example

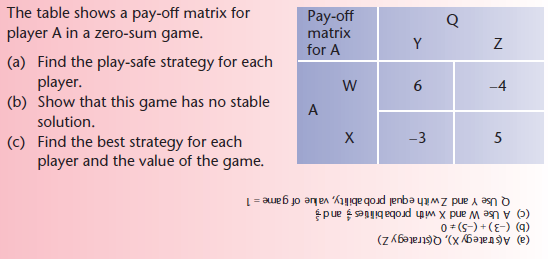
A and B are two players in a zero-sum game. A uses one of two strategies, W or X, and B uses one of the strategies Y or Z. The table shows the pay-off matrix for A.

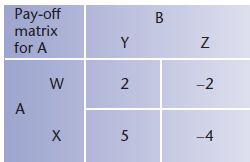
The pay-off matrix shows that if B adopts strategy Y then the pay-off for A will be 2 by using strategy W and 5 using strategy X.

On the other hand, if B adopts strategy Z then the pay-off for A will be 02 using strategy W and 04 using strategy X.

The idea is that neither player knows in advance which strategy the other will use.

The situation could equally be represented by the pay-off matrix for B. This would show corresponding values with opposite signs since this is a zero-sum game.

The play-safe strategy

The play-safe strategy for a player is the strategy for which the minimum pay-off is as high as possible. In the example above, the minimum pay-off for A using strategy W is 02, whereas the minimum pay-off using strategy X is 04. This means that strategy W is the play-safe strategy for player A.

Notice that finding the play-safe strategy for player A involves comparing the minimum values in the rows of the pay-off matrix for A.

Finding the play-safe strategy for B will involve comparing the values in the columns, remembering that B’s pay-offs are the negatives of the ones in the pay-off matrix for A.

The minimum value for B using strategy Y is 05 and the minimum value using strategy Z is 2. This means that the play-safe strategy for B is strategy Z.

The situation is shown in the pay-off matrices for A and B.

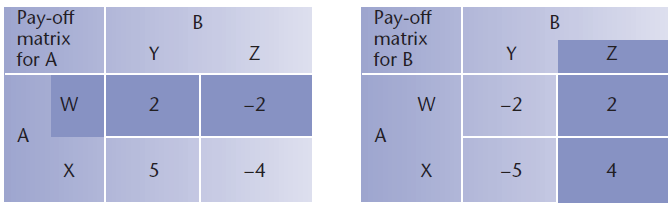
In this case, the maximum of the minimum pay-offs, for each player, is in the corresponding position in the two matrices. This represents the stable solution to the problem referred to as the saddle point (or minimax point).

The solution is stable in the sense that neither player can improve their pay-off by taking a different strategy, given that the other player doesn’t change.

In other words, while B uses strategy Z, the best strategy for A is W and while A uses strategy W, the best strategy for B is Z.

KEY POINT - If the sum of the two values used to determine the play-safe strategies is not zero then the values cannot correspond to the same cell position in the play-off matrices. This means that there is no saddle point and the game has no stable solution.

Example

The pay-off matrices for two players in a zero-sum game are given below. Show that there is no stable solution for the game.

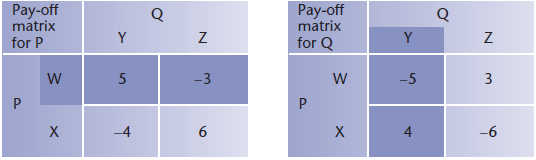
Optimal strategies for games that are not stable

The repeated use of the same strategy over a series of games is called a pure strategy. This provides the best results for both players in a game which has a stable solution. In the case where no stable solution exists, a mixed strategy is used in which each of the strategies is employed with a given probability to find the optimal solution.

Returning to the previous example:

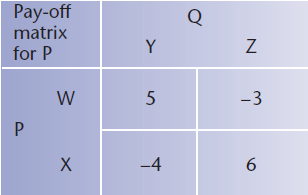
Graphical representation

Each graph corresponds to a strategy for Q (i.e. the opponent of P).

The diagram shows graphs of 9p − 4 and −9p + 6 against values of p from 0 to 1.

The point of intersection corresponds to the probability that gives the optimal mixed strategy for P in the last example.

KEY POINT - When P’s opponent has more strategies there will be more graphs with several points of intersection. You will need to identify the one that represents the optimal mixed strategy for P. This will be the highest point on or below each of the graphs.

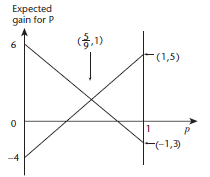
This diagram represents a situation where P’s opponent has three strategies to choose from.

The point representing the optimal mixed strategy for P is circled.

Notice how the problem of identifying the right vertex can be expressed as a linear programming problem in which the object is to maximise the expected gain for P subject to the constraints represented by the regions bounded by the straight line graphs.

This is, in fact, the approach used for higher dimensional problems. The conditions are formulated as a linear programming problem which may then be solved by the

simplex algorithm.

KEY POINT - If the pay-offs for one strategy are always better than the corresponding pay-offs for some other strategy then the weaker one can be ignored when determining the probabilities for a mixed strategy. In this way, the pay-off matrix is reduced by what is called a dominance argument.

PROGRESS CHECK

Log in