Projectiles

When a particle is projected from the ground it will follow a curved path, before hitting the ground. How far the particle travels will depend on the speed of projection and the angle of projection.

The suvat equations can be adapted to solve problems involving projectiles.

Let's examine the general case. A particle is projected at a speed of u (m/s) at an angle of a to the horizontal:

Image

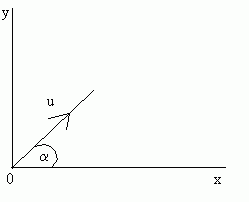
Range

The range (R) of the projectile is the horizontal distance it travels during the motion.

Now, s = ut + ½ at²

Using this equation vertically, we have that a = -g (the acceleration due to gravity) and the initial velocity in the vertical direction is usina (by resolving). Hence:

• y = utsina - ½ gt²       (1)

Using the equation horizontally:

• x = utcosa           (2)

Remember, there is no acceleration horizontally so a = 0 here.

When the particle returns to the ground, y = 0. Substituting this into (1):

0 = utsina - ½ gt²

t (usina - ½ gt) = 0

t = 0 or t = 2u sina         (3)

                   g

Therefore when x = R, t = 2u sina / g

Substituting into (2):

R = ucosa (2u sina)

               g

• The range is therefore

  Image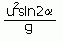

  

Time of Flight

The time the ball is in the air is given by (3).

Time of flight =

Image

Maximum Range

If a particle is projected at fixed speed, it will travel the furthest horizontal distance if it is projected at an angle of 45° to the horizontal. This is because the maximum sin2a can be is 1 and sin2a = 1 when a = 45°.

Velocity

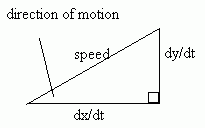
The velocity of the particle at any time can be calculated from the equation v = u + at.

By applying this equation horizontally, we find that:

• dx/dt = ucosa

By applying it vertically, we find that:

• dy/dt = usina - gt

To find the speed or direction of the particle at any time during the motion, find the horizontal and vertical components of the velocity using the above formulae and use Pythagoras's theorem:

Image

Example

A cannon ball is fired at an angle of 30° to the horizontal at a speed of 25ms^-1 .

a) How long will it be before the impact?

b) How far will the cannon ball travel before hitting the ground?

Image

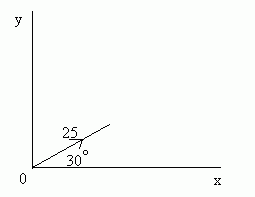
a) When the particle hits the ground, y = 0.

s = ut + ½ at²

Applying this equation vertically, when the particle hits the ground:

0 = 25Tsin30 - ½ gT² (Where T is the time of flight) 

Therefore, T(25sin30 - ½ gT) = 0

So T = 0 or T = (50sin30)/g

Therefore the time of flight is 2.55s (3sf) 

b) The range can be found working out the horizontal distance travelled by the particle after time T found in part (a)

s = ut + ½ at²

Applying this equation horizontally:

R = 25Tcos30

= 25 × 2.55 × 0.866

= 55.231...  

Therefore the horizontal distance travelled is 55.2m (3sf)