Simple Harmonic Motion
Simple Harmonic Motion arises when we consider the motion of a particle whose acceleration points towards a fixed point O and is proportional to the distance of the particle from O (so the acceleration increases as the distance from the fixed point increases).
As the particle moves away from the fixed point O, since the acceleration is pointing towards O, the particle will slow down and eventually stop (at Q), before returning to O. It will keep going and then again slow down as it reaches P before stopping at P and returning to O once more.
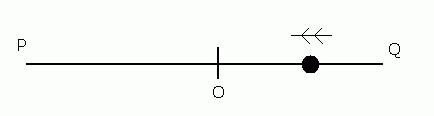
The particle will therefore move between two fixed points (P and Q). The amplitude of the motion is the distance from O to either P or Q (the distances are the same).
A particle which moves under simple harmonic motion will have the equation
-
= - w2x
where w is a constant (note that this just says that the acceleration of the particle is proportional to the distance from O).
You may be asked to prove that a particle moves with simple harmonic motion. If so, you simply must show that the particle satisfies the above equation.
Further Equations
We can solve this differential equation to deduce that:
-
v2 = w2(a2 - x2)
where v is the velocity of the particle, a is the amplitude and x is the distance from O.
From this equation, we can see that the velocity is maximised when x = 0, since v2 = w2a2 - w2x2
Hence the maximum velocity is aw (put x = 0 in the above equation and take the square root).
The period of the motion is the time it takes for the particle to perform one complete cycle. It can be calculated using:
-
T = 2p/w
If the particle is at 0 when t = 0, then the following equation also holds:
-
x = asin wt
If the particle is at P or Q when t = 0, then the following equation also holds:
-
x = acos wt
The Simple Pendulum
A simple pendulum consists of a particle P of mass m, suspended from a fixed point by a light inextensible string of length a, as shown here:

So we have approximate simple harmonic motion, where w2 = g/l .
