Stationary Points
Increasing and Decreasing Functions
An increasing function is a function where: if x1 > x2, then f(x1) > f(x2) , so as x increases, f(x) increases. A decreasing function is a function which decreases as x increases. Of course, a function may be increasing in some places and decreasing in others. A point where a function changes from an increasing to a decreasing function or visa-versa is known as a turning point. A turning point is a type of stationary point (see below).
We can use differentiation to determine if a function is increasing or decreasing:
A function is increasing if its derivative is always positive. A function is decreasing if its derivative is always negative.
Examples
y = -x has derivative -1 which is always negative and so -x is decreasing.
y = x2 has derivative 2x, which is negative when x is less than zero and positive when x is greater than zero. Hence x2 is decreasing for x<0 and increasing for x>0 .
Stationary Points
Stationary points are points on a graph where the gradient is zero. There are three types of stationary points: maximums, minimums and points of inflection (/inflexion). The three are illustrated here:
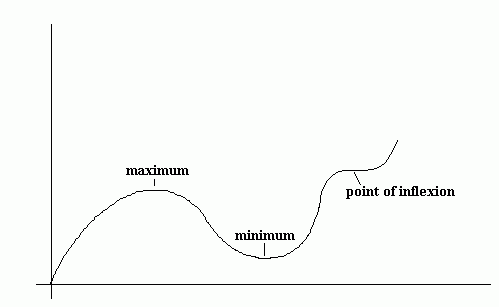
Example
Find the coordinates of the stationary points on the graph y = x2 .
We know that at stationary points, dy/dx = 0 (since the gradient is zero at stationary points).
By differentiating, we get: dy/dx = 2x. Therefore the stationary points on this graph occur when 2x = 0, which is when x = 0.
When x = 0, y = 0, therefore the coordinates of the stationary point are (0,0). In this case, this is the only stationary point. If you think about the graph of y = x2, you should know that it is "U" shaped, with its lowest point at the origin. This is what we have just found.
Maximum, Minimum or Point of Inflection?
At all the stationary points, the gradient is the same (= zero) but it is often necessary to know whether you have found a maximum point, a minimum point or a point of inflection. Therefore the gradient at either side of the stationary point needs to be looked at (alternatively, we can use the second derivative).
At maximum points, the gradient is positive just before the maximum, it is zero at the maximum and it is negative just after the maximum. At minimum points, the gradient is negative, zero then positive. Finally at points of inflexion, the gradient can be positive, zero, positive or negative, zero, negative. This is illustrated here:
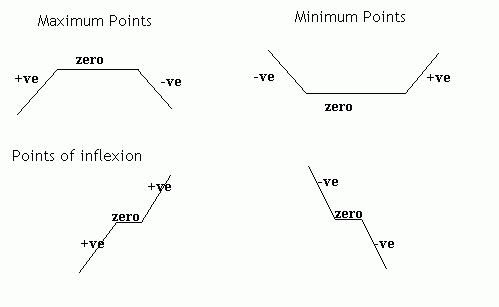
Example
Find the stationary points on the graph of y = 2x2 + 4x3 and state their nature (i.e. whether they are maxima, minima or points of inflexion).
dy/dx = 4x + 12x2
At stationary points, dy/dx = 0
Therefore 4x + 12x2 = 0 at stationary points
Therefore 4x( 1 + 3x ) = 0
Therefore either 4x = 0 or 3x = -1
Therefore x = 0 or -1/3
When x = 0, y = 0
When x = -1/3, y = 2x2 + 4x3 = 2(-1/3)2 + 4(-1/3)3 = 2/9 - 4/27 = 2/27
Looking at the gradient either side of x = 0:
When x = -0.0001, dy/dx = negative
When x = 0, dy/dx = zero
When x = 0.0001, dy/dx = positive
So the gradient goes -ve, zero, +ve, which shows a minimum point.
Looking at the gradient either side of x = -1/3 .
When x = -0.3334, dy/dx = +ve
When x = -0.3333..., dy/dx = zero
When x = -0.3332, dy/dx = -ve
So the gradient goes +ve, zero, -ve, which shows a maximum point.
Therefore there is a maximum point at (-1/3 , 2/27) and a minimum point at (0,0).
Solving Practical Problems
This method of finding maxima and minima is very useful and can be used to find the maximum and minimum values of all sorts of things.
Example
Find the least area of metal required to make a closed cylindrical container from thin sheet metal in order that it might have a capacity of 2000p cm3.
The total surface area of the cylinder, S, is 2pr2 + 2prh
The volume = pr2h = 2000p
Therefore pr2h = 2000p.
Therefore h = 2000/r2
Therefore S = 2pr2 + 2pr( 2000/r2 )
= 2pr2 + 4000p
r
So we have an expression for the surface area. To find when the surface area is a minimum, we need to find dS/dr .
dS = 4pr - 4000p
dr r2
When dS/dr = 0:
4pr - (4000p)/r2 = 0
Therefore 4pr = 4000p
r2
So 4pr3 = 4000p
So r3 = 1000
So r = 10
You should then check that this is indeed a minimum using the technique above.
So the minimum area occurs when r = 10. This minimum area is found by substituting into the equation for the area the value of r = 10.
S = 2pr2 + 4000p
r
= 2p(10)2 + 4000p
10
= 200p + 400p
= 600p
Therefore the minimum amount of metal required is 600p cm2
