Exponentials and Logarithms

The Exponential Function

The exponential function, written exp(x) or e^x, is the function whose derivative is equal to its equation. In other words:

Image

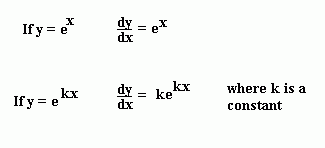
Because of this special property, the exponential function is very important in mathematics and crops up frequently.

Like most functions you are likely to come across, the exponential has an inverse function, which is log_ex, often written ln x (pronounced 'log x').

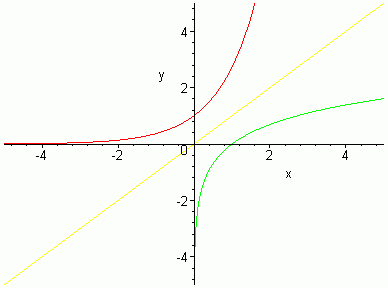
In the diagram, e^x is the red line, lnx the green line and y = x is the yellow line. Notice that lnx and e^x are reflections of one another in the line y = x .

Image

The Natural Logarithm

ln x is also known as the natural logarithm. The derivative of ln x is 1/x.

It therefore follows that the integral of 1/x is ln x + c .

Image

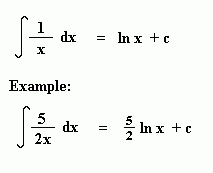
Solving Equations

If we are given equations involving exponentials or the natural logarithm, remember that you can take the exponential of both sides of the equation to get rid of the logarithm or take the natural logarithm of both sides to get rid of the exponential.

Example

Solve 0.5 = e^x

Then ln(0.5) = ln(e^x)

ln(0.5) = x