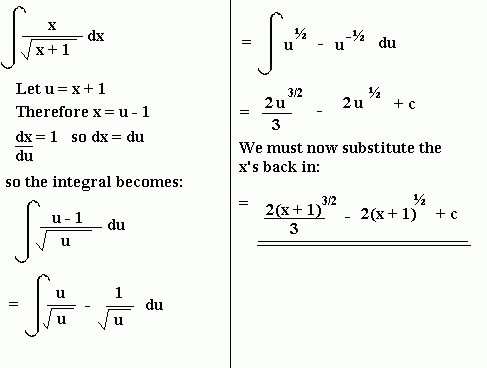Integration by Substitution

It is possible to transform a difficult integral to an easier integral by using a substitution. 

For example, suppose we are integrating a difficult integral which is with respect to x. We might be able to let x = sin t, say, to make the integral easier. As long as we change "dx" to "cos t dt" (because if x = sin t then dx/dt = cost) we can now integrate with respect to t and we will get the same answer as if we had done the original integral.

By using substitutions, we can show that:

Image

The second one is especially important. If you want to integrate a fraction, where the top is the differential of the bottom, the answer is simply ln of the bottom plus a constant.

Example

Find the integral of:

(a) -sin x cos²x

(b)    3x²  

      x³ + 1

(a) Using the first of the two above formulae above, imagine f(x) = cos x and n = 2. Therefore [f(x)]² = cos²x and f "(x) = -sin x. Therefore, since n = 2, the answer is simply (cos³x)/ 3 + c

(b) Since the top is the differential of the bottom, we can use the second of the two formulae above to get the answer of  ln(x³ + 1) + c.

Using a Substitution

Sometimes you will be told to integrate a function by using a substitution. Unless the substitution is simple, you will probably be told what substitution to use in the exam.

Example

Image