Integration Techniques

Important Formulae

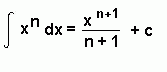
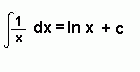
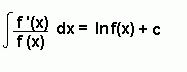
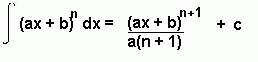
Rewriting the Integrand

Dividing

If you are asked to integrate a fraction, try multiplying or dividing the top and bottom of the fraction by a number.

Example

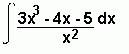
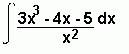
If we divide everything on the numerator and everything on the denominator by x², we get:

= ∫ (3x – 4x^-1 – 5x^-2) dx

= 3x² – 4lnx + 5x^-1 + c

2

Split into Partial Fractions

Sometimes it will help if you split a fraction up before attempting to integrate. This can be done using the method of partial fractions.

Example

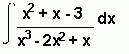
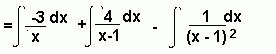
(Here we split the fraction into partial fractions)

= -3lnx + 4ln(x - 1) + (x - 1)^-1 + c

Using Trigonometric Formulae

When integrating trigonometric expressions, it will often help to rewrite the integral using trigonometric formulae.

Example

∫ cos²x dx

cos2x = 2cos²x - 1

cos²x = ½ (cos2x + 1)

∫ cos²x dx = ½ ∫ (cos2x + 1) dx

= ½ ( ½ sin2x + x) + c

= ¼ sin2x + ½ x + c

Log in