Radians

Radians, like degrees, are a way of measuring angles.

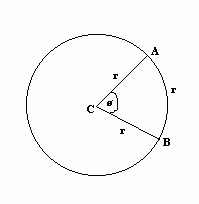
One radian is equal to the angle formed when the arc opposite the angle is equal to the radius of the circle. So in the above diagram, the angle ø is equal to one radian since the arc AB is the same length as the radius of the circle.

The video below shows you how to convert radians and degrees.

Now, the circumference of the circle is 2 PI r, where r is the radius of the circle. So the circumference of a circle is 2 PI larger than its radius. This means that in any circle, there are 2 PI radians.

Therefore 360º = 2 PI radians.

Therefore 180º = PI radians.

So one radian = 180/ PI degrees and one degree = PI /180 radians.

Therefore to convert a certain number of degrees in to radians, multiply the number of degrees by PI /180 (for example, 90º = 90 × PI /180 radians = PI /2). To convert a certain number of radians into degrees, multiply the number of radians by 180/ PI .

Arc Length

The length of an arc of a circle is equal to ∅, where ∅ is the angle, in radians, subtended by the arc at the centre of the circle (see below diagram if you don’t understand). So in the below diagram, s = r∅ .

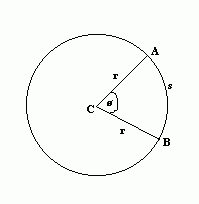
Area of Sector

The area of a sector of a circle is ½ r² ∅, where r is the radius and ∅ the angle in radians subtended by the arc at the centre of the circle. So in the below diagram, the shaded area is equal to ½ r² ∅ .

Log in