Bayes' Theorem

Bayes' Theorem says that:

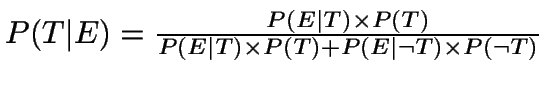
Note that the union of all of the As (A1, A2, ... An) = the total sample space, so they cover every possibility.

Example

There are two bags containing balls of various colours. A bag is selected at random and a ball taken from it at random. The probability of picking a blue ball out of bag 1 is ½ . The probability of picking a blue ball from bag 2 is ¼ . If the experiment is carried out and a blue ball is selected, what is the probability that bag 2 was selected?

Let A2 be the event that bag 2 was selected and let A1 be the event that bag one was selected. Let B be the event that a blue ball is chosen. Then, using Bayes' Theorem:

P(A2|B) = P(B|A2)P(A2) .

P(B|A1)P(A1) + P(B|A2)P(A2)

Now, P(B|A2) = probability of picking a blue ball given that bag A2 is selected = ¼ from the question.

Similarly, P(B|A1) = ½ .

P(A1) = probability of selecting bag 1 = ½ = P(A2)

Hence P(A2|B) = ¼ × ½.

½ × ½ + ¼ × ½

= 1/3

Log in