Skewness

A normal distribution is a bell-shaped distribution of data where the mean, median and mode all coincide. A frequency curve showing a normal distribution would look like this:

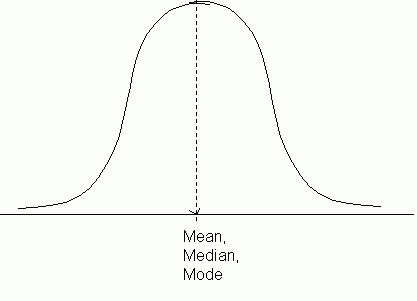
In a normal distribution, approximately 68% of the values lie within one standard deviation of the mean and approximately 95% of the data lies within two standard deviations of the mean.

If there are extreme values towards the positive end of a distribution, the distribution is said to be positively skewed. In a positively skewed distribution, the mean is greater than the mode. For example:

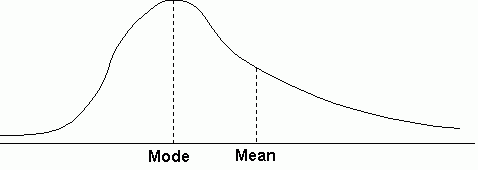
A negatively skewed distribution, on the other hand, has a mean which is less than the mode because of the presence of extreme values at the negative end of the distribution.

There are a number of ways of measuring skewness:

Pearson’s coefficient of skewness	=	mean – mode	=	3(mean – median)
		Standard deviation		Standard deviation

Quartile measure of skewness	=	Q₃ – 2Q₂ + Q₁
		Q₃ – Q₁

Log in