Uniform Distribution

A continuous random variable X which has probability density function given by:

f(x) = 1   for a £ x £ b

         b - a

(and f(x) = 0 if x is not between a and b) follows a uniform distribution with parameters a and b. We write X ~ U(a,b)

Image

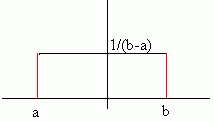
Remember that the area under the graph of the random variable must be equal to 1 (see continuous random variables).

Expectation and Variance

If X ~ U(a,b), then:

• E(X) = ½ (a + b)

• Var(X) = (1/12)(b - a)²

Proof of Expectation

Image

Cumulative Distribution Function

The cumulative distribution function can be found by integrating the p.d.f between 0 and t:

Image