Elastic Properties of Solids
Under Stress
Hooke’s Law
“Forces can cause objects to deform (i.e. change their shape). The way in which an object deforms depends on its dimensions, the material it is made of, the size of the force and direction of the force.”
F = ke
Where:
F = tension acting on the spring.
e is extension = (l-lo); l is the stretched length and lo is original length.
k = the spring constant.
Image
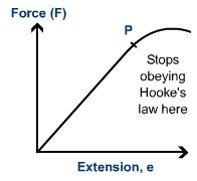
Once the spring is extended beyond the point P, it will no longer return to its original shape. This is the point of elastic limit.
If a material returns to its original shape after forces are applied, it demonstrates elastic behaviour.
If a material deforms from its original shape after forces are applied, it is a sign of plastic behaviour.
Elastic Potential Energy
“If the deformation caused is within the elastic limit, the work done in deforming the object is stored within it as potential energy. This is called (elastic) ‘strain energy’. When the applied force is removed the energy is released. The strain energy then performs work in changing the object and to its original state.”
Image
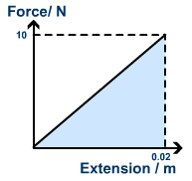
The work done (W) by the object is the shaded triangular area under the straight line.
Stress, strain and Young’s Modulus
Stress is defined as the force per unit area of a material:
Stress = force/cross sectional area
where s = stress, F = force applied, A= cross sectional area
Units of s: Nm-2 or Pa.
Strain is defined as extension per unit length:
Strain = extension/original length
where e = strain, lo = the original length, e = extension = (l-lo) and l = stretched length
Strain has no units because it is a ratio of lengths.
Image
The gradient of the straight-line graph is the Young’s modulus, E
Image
Units of the Young modulus E: Nm-2 or Pa
Category
