Gravitational fields

After studying this section you should be able to:

understand the concept of a field
recall and use the relationship that describes the gravitational force between two masses
describe the Earth’s gravitational field and explain how the field strength varies with distance from the centre of the Earth

The following sections can be found below

Fields
Gravitational Fields
Universal Gravitation
g and G
Potential Energy
Calculating Potential Energy
Equipotential Surfaces
Calculating Potential

Fields

A field is a region of space where forces are exerted on objects with certain properties. In this and subsequent sections three types of field are considered:

gravitational fields affect anything that has mass
electric fields affect anything that has charge
magnetic fields affect permanent magnets and electric currents.

These three types of field have many similar properties and some important differences. There are key definitions and concepts that are common to all three types of field.

Radiant energy such as light has mass and so is affected by gravitational fields.

Gravitational fields

Newton realised that all objects with mass attract each other. This seems surprising, since any two objects placed close together on a desktop do not immediately move together. The attractive force between them is tiny, and very much smaller than the frictional forces that oppose their motion.

Gravitational attractive forces between two objects only affect their motion when at least one of the objects is very massive. This explains why we are aware of the force that attracts us and other objects towards the Earth – the Earth is very massive. The mass of the Earth is

about 6 × 10²⁴ kg.

The diagram represents the Earth’s gravitational field. The lines show the direction of the force that acts on a mass that is within the field.

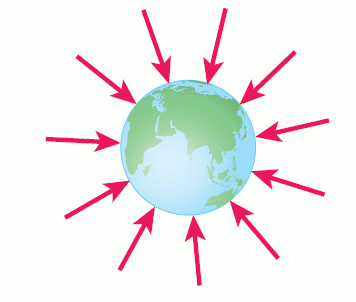
This diagram shows that:

gravitational forces are always attractive – the Earth cannot repel any objects
the Earth’s gravitational pull acts towards the centre of the Earth
the Earth’s gravitational field is radial; the field lines become less concentrated with increasing distance from the Earth.

The force exerted on an object in a gravitational field depends on its position. The less concentrated the field lines, the smaller the force. If the gravitational field strength at any point is known, then the size of the force can be calculated.

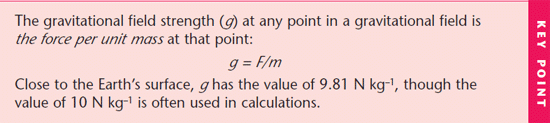
Gravitational field strength is a vector quantity: its direction is towards the object that causes the field.

Always use the given value for g. Candidates often lose marks for using 10ms^–2 when the formula sheet gives g = 9.81ms^–2

Universal gravitation

In studying gravitation, Newton concluded that the gravitational attractive force that exists between any two masses:

is proportional to each of the masses
is inversely proportional to the square of their distances apart.

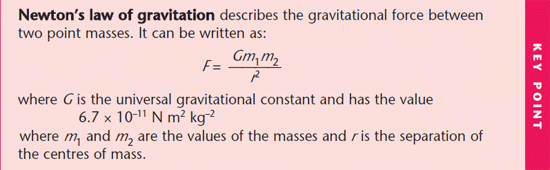
A point mass is one that has a radial field, like that of the Earth.

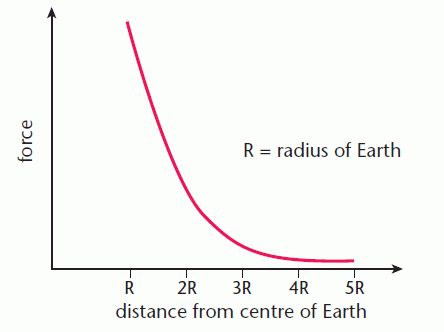
Although the Earth is a large object, on the scale of the Universe it can be considered to be a point mass. The gravitational field strength at its centre is zero, since attractive forces pull equally in all directions. Beyond the surface of the Earth, the gravitational force on an object decreases with increasing distance. When the distance is measured from the centre of the Earth, the size of the force follows an inverse square law; doubling the distance from the centre of the Earth decreases the force to one quarter of the original value. The variation of force with distance from the centre of the Earth is shown in the diagram.

Remember that two objects attract each other with equal-sized forces acting in opposite directions.

g and G

Newton’s law of gravitation can be used to work out the value of the force between any two objects. It can also be used to calculate the strength of the gravitational field due to a spherical mass such as the Earth or the Sun.

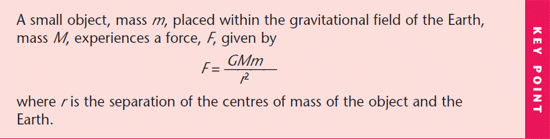
A negative sign is sometimes used on the right-hand side of this equation, following the convention that attractive forces are given negative values and repulsive forces positive values.

It follows from the definition of gravitational field strength as the force per unit mass that the field strength at that point, g, is related to the mass of the Earth by the expression:

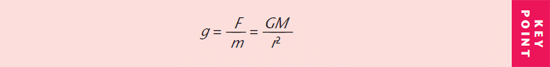
Gravitational field strength is a property of any point in a field. It can be given a value whether or not a mass is placed at that point. Like gravitational force, beyond the surface of the Earth the value of g follows an inverse square law.

Because the inverse square law applies to values of g when the distance is measured from the centre of the Earth, there is little change in its value close to the Earth’s surface. Even when flying in an aircraft at a height of 10 000 m, the change in distance from the centre of the Earth is minimal, so there is no noticeable change in g. The radius of the Earth is about 6.4 × 10⁶ m, so you would have to go much higher than

aircraft-flying height for g to change by 1%.

The same symbol, g, is used to represent:

gravitational field strength
free-fall acceleration.

These are not two separate quantities, but two different names for the same quantity. Gravitational field strength, g, is defined as the force per unit mass, g = F/m.

From Newton’s second law and the definition of the newton, free-fall acceleration, g, is also equal to the gravitational force per unit mass. The units of gravitational field strength, N kg^–1, and free-fall acceleration, m s^–2, are also equivalent.

Potential and potential energy

When an object changes its position relative to the Earth, there is a change in potential energy given by ΔE_p = mgΔh. It is not possible to place an absolute value on the potential energy of any object when h is measured relative to the surface of the Earth. Two similar objects placed at the top and bottom of a hill have different values of potential energy, but relative to the ground the potential energy is zero for both objects.

Absolute values of potential energy are measured relative to infinity. In this context, infinity means ‘at a distance from the Earth where its gravitational field strength is so small as to be negligible’.

On an absolute scale of measurement, zero must be the smallest possible value and ‘20 units’ must be twice as much as ‘10 units’.

The car at the top of the hill has more potential energy than the one at the bottom, but relative to ground level they both have zero.

Using this reference point:

all objects at infinity have the same amount of potential energy, zero
any object closer than infinity has a negative amount of potential energy, since it would need to acquire energy in order to reach infinity and have zero energy.

Work has to be done to move an object from within the Earth’s gravitational field to infinity.

Just as gravitational field strength is used to place a value on the gravitational force that would be experienced by a mass at any point in a gravitational field, the concept of gravitational potential is used to give a value for the potential energy.

KEY POINT - The gravitational potential at a point in a gravitational field is the potential energy per unit mass placed at that point, measured relative to infinity.

So if the potential at any point in a field is known, the potential energy of a mass placed at that point can be calculated by multiplying the potential by the mass.

Calculating potential and potential energy

When an object is within the gravitational field of a planet, it has a negative amount of potential energy measured relative to infinity. The amount of potential energy depends on:

the mass of the object
the mass of the planet
the distance between the centres of mass of the object and the planet.

The centre of mass of a planet is normally taken to be at its centre.

KEY POINT - The gravitational potential energy measured relative to infinity of a mass, m, placed within the gravitational field of a spherical mass M can be calculated using:

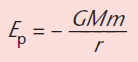
where r is the distance between the centres of mass and G is the universal gravitational constant. Gravitational potential energy is measured in joules (J).

Since gravitational potential is the gravitational potential energy per unit mass placed at a point in a field, it follows that:

KEY POINT - Gravitational potential, V, is given by the relationship:

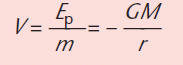
Gravitational potential is measured in J kg^–1.

The relationship between potential and potential energy is similar to that between gravitational force and gravitational field strength:

potential and field strength are properties of a point in a field
potential energy and force are the corresponding properties of a mass placed within a field.

Equipotential surfaces

The potential energy of a satellite in a circular orbit around the Earth remains constant provided that its distance from the centre of the Earth does not change. To move to a higher or lower orbit the satellite must gain or lose energy. The satellite travels along an equipotential surface, the spherical shape consisting of all points at the same potential.

The diagram shows the spacing of equipotential surfaces around the Earth. The surfaces are drawn at equal differences of potential.

For a satellite in an elliptical orbit, there is an interchange between kinetic and potential energy as it travels around the Earth.

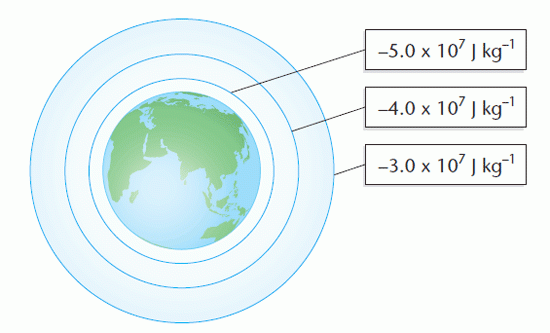
The diagram shows that:

equipotential surfaces around a spherical mass are also spherical
the spacing between the equipotential surfaces increases with increasing distance from the centre of the Earth.

For a satellite to move from an orbit where the potential is – 4.0 × 10⁷ J kg^–1 to one where the potential is – 3.0 × 10⁷ J kg^–1, it needs to gain 1.0 × 10⁷ J of gravitational potential energy for each kilogram of satellite. It does this by firing the rocket engines, transferring energy from its fuel supply.

To move to a lower orbit, a rocket can lose energy by firing the rocket engines ‘backwards’ so that the exhaust gases are expelled in the direction of motion.

Calculating potential

The value of the gravitational potential at a point in a gravitational field depends on:

the mass of the object causing the field
the distance from the centre of mass of this object.

KEY POINT - The gravitational potential, V, due to a spherical mass, M, at a distance r from its centre of mass is given by:

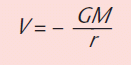
The diagram above shows that the rate of change of potential with distance, the potential gradient, decreases with increasing distance from the Earth.

As the potential gradient decreases, so does the gravitational field strength.

KEY POINT - The relationship between gravitational field strength and potential gradient is:

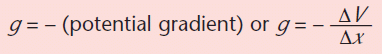
where ΔV is the change in potential over a small distance Δx.

The concept of potential gradient is similar to that of the gradient of a hill or slope. The steeper the slope, the greater the acceleration of an object free to move down it.

PROGRESS CHECK

Log in