Boolean Logic
This section explains Boolean Logic focusing on: Why data is represented in binary form, AND gates, OR gates, NOT gates and Combining gates.
Why Data is Represented in Binary Form
State
Computers use binary (base 2) to represent data because they operate with two states:
ON (1): Represents high voltage or presence of power.
OFF (0): Represents low voltage or absence of power.
These states align naturally with the digital circuits that underpin computing hardware.
Logic Gates
Logic gates are the building blocks of digital circuits. They process binary inputs (0s and 1s) to produce binary outputs.
Logic gates work based on Boolean algebra.
Boolean Algebra
Boolean algebra is a mathematical system for binary values, introduced by George Boole.
It uses operations like AND, OR, and NOT to perform logical reasoning.
Boolean logic is fundamental to decision-making in programs and hardware.
Basic Logic Gates
Logic gates take one or more binary inputs and produce a single binary output based on logical rules.
AND Gate
Operation: Produces an output of 1 only if both inputs are 1.
Truth Table:
| Input A | Input B | Output (A AND B) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Symbol:
A diagrammatic representation of an AND gate looks like a "D" shape.
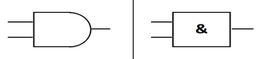
OR Gate
Operation: Produces an output of 1 if either input is 1.
Truth Table:
| Input A | Input B | Output (A AND B) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Symbol:
A diagrammatic representation of an OR gate looks like a curved shield.
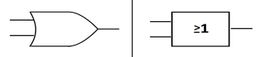
NOT Gate
Operation: Produces the opposite of the input.
If the input is 1, the output is 0, and vice versa.
Truth Table:
| Input A | Output (NOT A) |
| 0 | 1 |
| 1 | 0 |
Symbol:
A triangle with a circle at the tip.
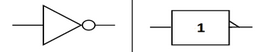
Combining Gates
Logic gates can be combined to form more complex circuits and logical operations.
Combining Two AND Gates
Two AND gates can be connected to process multiple inputs.
Example:
If inputs A and B pass through an AND gate, and inputs C and D pass through another, their outputs can be processed further by another gate.
Truth Table:
| A | B | A AND B | C | D | C AND D | Final Output (A AND B) AND (C AND D) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Combining OR and NOT Gates
Combining OR and NOT gates allows for more advanced logic.
Example:
The output of an OR gate can be inverted by a NOT gate.
This creates a NOR gate (NOT OR), which produces 1 only if all inputs are 0.
Truth Table for NOR Gate:
| A | B | A OR B | NOT (A OR B) |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Applications of Boolean Logic
Computer Circuits: Used in CPUs, memory devices, and other digital hardware.
Programming: Boolean logic underpins decision-making in code.
Problem Solving: Boolean algebra simplifies complex conditions in algorithms.
Summary of Key Concepts
Binary Representation: Computers use binary states (1 and 0) because of their digital nature.
Basic Logic Gates: AND, OR, and NOT gates form the foundation of Boolean logic.
Combining Gates: Complex circuits can be created by combining basic gates, such as creating a NOR gate by combining OR and NOT.
Boolean Algebra: Provides a mathematical framework for logical operations, essential in both software and hardware.
Boolean logic ensures precise and efficient decision-making, making it critical in both theoretical and practical aspects of computer science.
