Tangents

There are two theorems for tangents that you need to know.

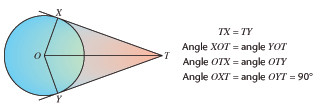
(a) Tangents drawn from the same point to the same circle are equal in length. They subtend equal angles at the centre of the circle and they make equal angles with the straight line joining the centre of the circle to the point.

(b) The angle between a tangent and a chord drawn from the point of contact is equal to any angle subtended by the chord in the alternate segment.

Angle BXT = angle BAX

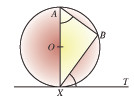
This fact can be proved as follows:

Angle ABX = 90° (angle in a semicircle)
Angle OXT = 90° (angle between a diameter and a tangent)
Angle AXB = 90° - angle BXT
but angle AXB + angle BAX + angle ABX = 180° (angle sum of triangle)
ie angle AXB + angle BAX = 90°
Therefore 90° - angle BXT + angle BAX = 90°
Therefore angle BXT = angle BAX

Examples

(a) Find angle a

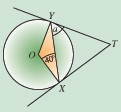
Angle OYT = 90°
Angle OYX = 40° (isosceles triangle)
Therefore angle a = 50°

(b) Find angles a and b.

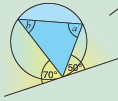
Angle a = 70°
Angle b = 50° (both are angles in alternate segment)

The video below highlights the rules you need to remember to work out circle theorems.

Log in