After studying this section, you will be able to:
- use the angle sum of a triangle and a quadrilateral
- identify quadrilaterals by their geometric properties
The video below looks at the properties of triangles and quadrilaterals.
Sum of angles of a triangle
You need to be able to prove that:
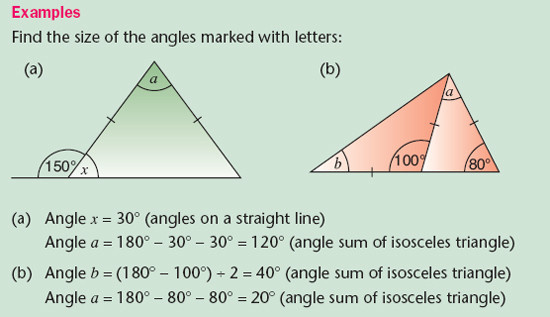
(a) the sum of the angles in a triangle is 180°.
Take any triangle ABC. Construct XY through B and parallel to AC. Using the properties of parallel
lines angle A = angle XBA and angle C = angle CBY. Hence the angle sum of the triangle is angle A + angle ABC + angle C = angle XBA + angle ABC + angle CBY = 180° = angles on a straight line.
You must remember the basic angle facts such as the sum of the angles on a straight line is 180°, and the properties of alternate and corresponding angles.
Image
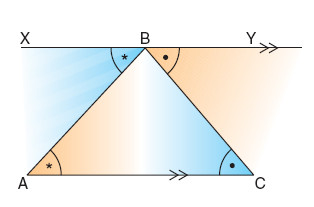
(b) the exterior angle of a triangle is equal to the sum of the interior opposite angles.
Take any triangle ABC. Construct a line through C, parallel to AB.
angle p = angle b (corresponding angles)
angle s = angle a (alternate angles)
Therefore angle p + angle s = angle a + angle b
but angle r = angle a + angle b
Therefore angle p + angle s = angle r
Image
Properties of quadrilaterals
Sum of angles in a quadrilateral
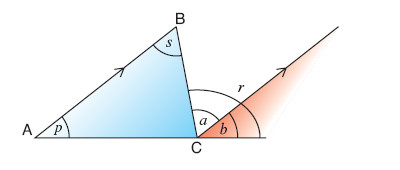
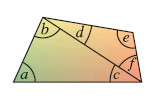
You can use the fact that the sum of the angles in a triangle = 180° to prove that the angle sum of a quadrilateral is 360°.
angles a + b + c = 180°
angles d + e + f = 180°
Therefore a + b + c + d + e + f = 360°
Image
Geometric properties of quadrilaterals
You need to be able to identify quadrilaterals by their geometric properties.
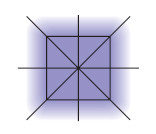
(a) Square
- all sides equal and opposite sides parallel
- all angles 90°
- four lines of symmetry
- rotational symmetry order 4
- diagonals bisect at right angles
Image
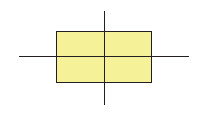
(b) Rectangle
- opposite sides equal and parallel
- all angles 90°
- two lines of symmetry
- rotational symmetry order 2
Image
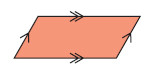
(c) Parallelogram
- opposite sides equal and parallel
- opposite angles equal
- no lines of symmetry
- rotational symmetry order 2
Image
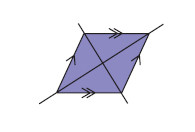
(d) Rhombus
- all sides equal
- opposite sides parallel
- two lines of symmetry
- rotational symmetry order 2
- diagonals bisect at right angles
Image
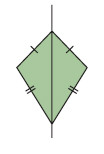
(e) Kite
- one line of symmetry
- diagonals intersect at right angles
Image
(f) Trapezium
- one pair of sides parallel
Image
Image
