Sine, cosine and tangent of any angle
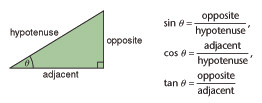
You already know that, in a right-angled triangle, the sine, cosine and tangent are defined as:
Image
You should also know that it is possible to define the trigonometric ratios for angles of any size using coordinates.
Draw a circle with radius 1 unit. The point P with coordinates (x , y) moves round the circumference of the circle. OP makes an angle θ with the positive x-axis. The angle increases as P rotates anticlockwise. For any angle θ the sine, cosine and tangent are given by the coordinates of P.
Image
Image
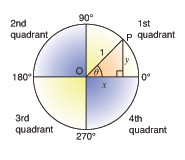
Notice that as P rotates the coordinates change sign.
- In the first quadrant, from 0° to 90° both y and x are positive.
- In the second quadrant from 90° to 180° y is positive but x is negative.
- In the third quadrant, from 180° to 270° both y and x are negative.
- In the fourth quadrant, from 270° to 360° y is negative but x is positive.
Thus the sign of the sine, cosine and tangent of an angle changes according to
Image
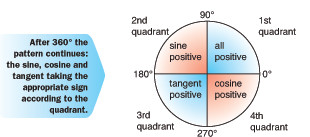
the size of the angle, that is the sign depends on which quadrant the angle is in.
The graphs of the three ratios, sine, cosine and tangent are shown in Figures 1, 2 and 3. You need to recognise them and distinguish between them.
Image
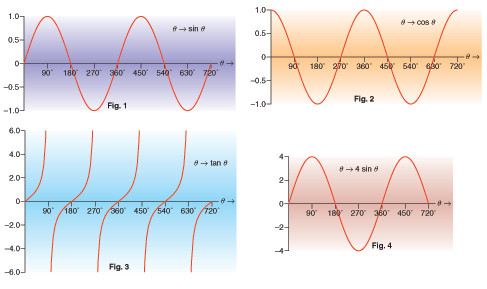
The sine curve models many natural phenomena including sound and light waves. Because it repeats every 360° the graph is described as periodic with period 360°. (The other curves are similarly periodic with periods 360° for the cosine and 180° for the tangent.) Note that the tangent curve is of a different form and at 90°, 270°, 450° etc. the value of the tangent is infinity and hence cannot be plotted.
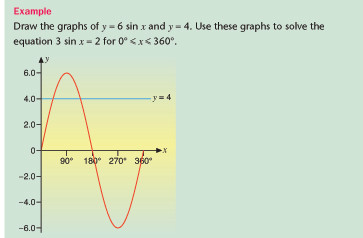
The graph of sin θ oscillates between 01 and !1. This means that the amplitude of the sine curve is 1. The amplitude can be changed by multiplying sin θ by a number, for example 4. The graph of 4 sin θ is shown in Figure 4.
You can use graphs like these to solve equations involving trigonometrical functions.
Image
Image
Category
