Pythagoras Theorem

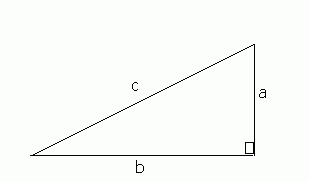
In any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

i.e.: c² = a² + b² in the following diagram:

Example

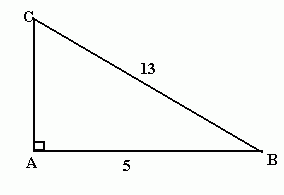
Find AC in the diagram below.

AB² + AC² = BC²

AC² = BC² - AB²

= 13² - 5²

= 169 - 25 = 144

AC = 12cm

This video explains how to work out phytagoras theorem

3D Problems (Higher Tiers)

In higher tier papers, you may be asked to solve 3d problems using Pythagoras.

Example

A cuboid has sides of length 10cm, 2 √11 cm and 5cm. Find the length of a diagonal.

So we want to find AD.

We can draw a right-angled triangle inside the cuboid which has AD as it's hypotenuse. Then we can use Pythagoras.

To use Pythagoras, we need to know AC and CD. We know that CD is 5 cm. We need to find AC.

We can use Pythagoras to find AC, because if we look at the cuboid from above, we see that AC is the diagonal of a rectangle

ABC is a right angled triangle, so by Pythagoras, AC² = AB² + BC²

= 10² + (2 √11)² = 100 + 44 = 144

Now we can find AD: AD² = AC² + CD² = 144 + 25 = 169

Therefore AD = 13

Log in