Integration by Parts

From the product rule, we can obtain the following formula, which is very useful in integration:

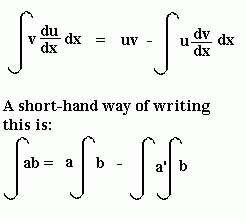
It is used when integrating the product of two expressions (a and b in the bottom formula). When using this formula to integrate, we say we are "integrating by parts".

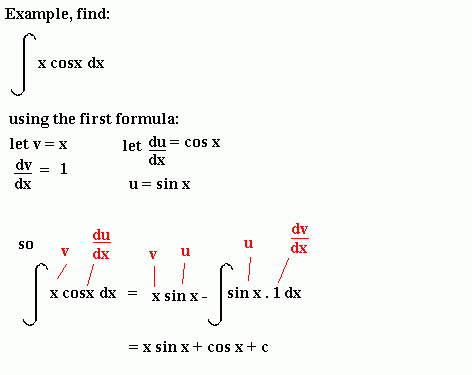
Sometimes you will have to integrate by parts twice (or possibly even more times) before you get an answer.

Example

Find ∫xe^-x dx

Integrating by parts (with v = x and du/dx = e^-x), we get:

-xe^-x - ∫-e^-x dx (since ∫e^-x dx = -e^-x)

= -xe^-x - e^-x + constant

We can also sometimes use integration by parts when we want to integrate a function that cannot be split into the product of two things. The trick we use in such circumstances is to multiply by 1 and take du/dx = 1.

Example

Find ∫ ln x dx

To integrate this, we use a trick, rewrite the integrand (the expression we are integrating) as 1.lnx . We then let v = ln x and du/dx = 1 .

Hence ∫ ln x dx = x ln x - ∫ x (1/x) dx

= x lnx - ∫ dx

= x lnx - x + constant

Log in