Queues

After studying this section you should be able to:

explain the concept of a queue
describe methods of representing a queue
describe the algorithms used to manipulate a queue

Implementing queues

A queue is a FIFO structure in that it adds items to the back of the queue and takes items from the front. If this is implemented as a linked list the linked list operations will take care of this, but an array implementation needs a special approach. The items can be stored in an array together with two variables:

Front – to indicate the item at the front of the queue
Rear – to indicate the item at the back of the queue.

It can also be useful to have two additional variables:

NoInQ – number of items in the queue
MaxSize – the maximum size of the queue.

Let us suppose we have a queue containing Terry, Lim, Mark and Tamsin

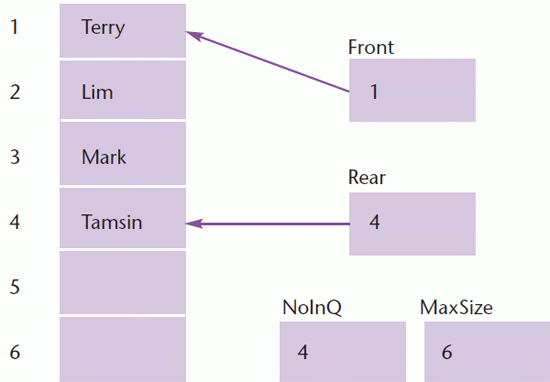
As items are added and removed the items move down the array until they reach the end. Let us assume that Terry, Lim and Mark are removed and Ursula and Norma are added.

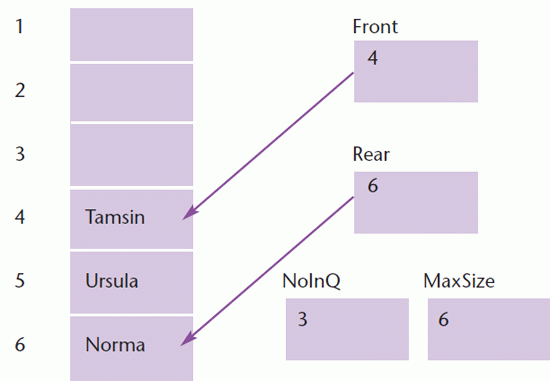
The next item must be added in position 1. We say that we are implementing a circular array. A procedure to add an element to such a queue might be:

PROCEDURE ADD(inItem)

     IF NoInQ = MaxSize

          THEN output "Queue Full"

     ELSE

          IF Rear = 6

               THEN Rear := 1

          ELSE

               Add 1 to Rear

          ENDIF

(A better solution is Rear := (Rear Mod 6) + 1)

          Queue[Rear] := inItem

          Add 1 to NoInQ

     ENDIF

ENDPROC

In this case an even better solution would use MaxSize in place of the integer 6.

Log in