Sorting and searching algorithms

After studying this section you should be able to:

• understand algorithms to search for an item
• describe methods of sorting data
• explain how to merge two sets of data

The different types of sort and search

Searching algorithms are used to find an item in a list. The algorithm will be given the key of the item to be found and the search will work through the list looking

for a match.

Sorting algorithms are used to place a list of items into key sequence (either ascending or descending).

Linear search

A procedure to search an ordered list of items for an item can be performed by starting with the first item and proceeding through the list until the item is found.

The search is completed when the item is found or when it comes across an item that has a larger valued key than the required item. An algorithm to search an array

Arr might be:

PROCEDURE LinearSearch(RequiredItem)

     Found := false

     Failed := false

     Current := 1

     WHILE (Current <= MaxSize) AND (Found = false) AND (Failed = false)

          IF RequiredItem = Arr[Current] THEN Found := true

          ELSE

               IF RequiredItem < Arr[Current] THEN

                    Add 1 to Current

                    IF Current > MaxSize THEN Failed := true

                    ENDIF

               ELSE Failed := true

               ENDIF

          ENDIF

     ENDWHILE

ENDPROC

Binary search

A linear search requires that, on average, half the items will be inspected. A binary search is more efficient. It operates on the principle that the middle item divides the list into two halves. By inspecting the middle item the program can establish which half contains the required item. The algorithm continues by repeating the process on the half that contains the required item. A pseudocode procedure to perform this process is given below.

A binary search is dramatically faster than a linear search when there are a large number of items.

/* Low is the number of the first element in the array and

High is the number of the last element */

PROCEDURE BinarySearch(Low, High, RequiredItem)

     Found := False

     REPEAT

          Middle := Integer part of ((Low + High)/2)

          IF Arr[Middle] = RequiredItem

               THEN Found := true

          ELSE IF Arr[Middle] > RequiredItem

                    THEN High := Middle – 1

                ELSE Low := Middle + 1

                ENDIF

          ENDIF

       UNTIL (Found = True) OR (Low > High)

ENDPROC

Merging

It is often necessary to merge two lists of items. This can only be done efficiently if the lists are both in the same sequence. The algorithm is simpler if terminating values that are larger than any value in the lists are added to the end of the lists before the merge takes place. A pseudocode procedure to merge two lists into a third is as follows:

PROCEDURE Merge(Arr1,Arr2,Arr3)

     Current1 := 1

     Current2 := 1

     Current3 := 1

     WHILE Arr1[Current1] is not a terminator

          OR Arr2[Current2] is not a terminator do

          IF Arr1[Current1] < Arr2[Current2]

               THEN

                    Arr3[Current3] := Arr1[Current1]

                    Add 1 to Index1

               ELSE

                    Arr3[Current3] := Arr2[Current2]

                    Add 1 to Index2

          ENDIF

          Add 1 to Index3

     ENDWHILE

ENDPROC

Bubble sort

The bubble sort is not very efficient but it is simple to program and a useful algorithm when there are not many items involved. The bubble sort performs a number of passes through the items, each pass putting the items into a slightly better sequence. During a pass the algorithm compares each item with the following item and, if they are out of sequence, it swaps their positions. The effect is shown below.

Merging can equally apply to sequential files. The bubble sort is so called as the small numbers bubble slowly to the surface while the large numbers drop like stones to the bottom.

Image

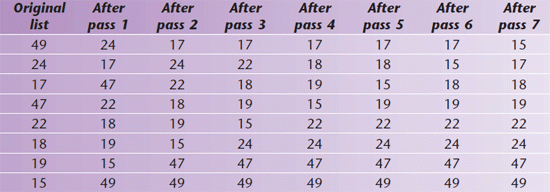
The maximum number of passes required to obtain a correct sequence is N–1, where N is the number of items. The algorithm can be improved by halting if no items are swapped during a pass. This improved algorithm might be:

PROCEDURE Bubblesort

     Pass := 1

     REPEAT

          SwapFlag := false

          FOR Count := 1 TO NoOfItems

               IF Arr[Count] > Arr[Count+1] THEN

                    Temp := Arr[Count]

                    Arr[Count] := Arr[Count+1]

                    Arr[Count+1] := Temp

                   SwapFlag := true

              ENDIF

          ENDFOR

          Add 1 to Pass

     UNTIL Pass = NoOfItems OR SwapFlag = false

ENDPROC

Insertion sort

The insertion sort is an improvement on the bubble sort but it is still relatively slow and suitable only when there is a limited number of items. The items are copied into a new array one at a time. Each item is inserted in the correct place and all the succeeding items that are already in the new array are moved up one place to make space. It is generally more efficient to start at the end of the list, rather than the start, when inserting.

Quicksort

As its name might suggest, the quicksort is, indeed, very fast. It operates as follows:

• 1 - Select an item at random (often the last item).
• 2 - Create two new lists of items, one with all the items smaller than the chosen item and the other with the rest.
• 3 - Repeat step 1 with each list until the lists have a single item.

You should not be asked to write a quicksort algorithm but you may have to trace one.